To Remember
Definition of CongruenceThe Theorem on page 137 follows logically from this definition plus the property of substitution.
Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.
If triangle ABC is congruent to triangle DEF, the relationship can be written mathematically as:
In many cases it is sufficient to establish the equality of three corresponding parts and use one of the following results to deduce the congruence of the two triangles.
Watch the tutorial:
Two triangles congruent to a third triangle are congruent to each other.
Do:
- Set I, 6-11, 12-17
- Set II, odd numbers
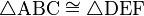
No comments:
Post a Comment
Put your initials or something here when you have finished the lesson.